Rhythm Necklaces &
Euclidean Distribution

Gilbert Rouget
Music & Trance
University of Chicago Press, 1985
Music & Trance
University of Chicago Press, 1985

Bruno Latour
We Have Never Been Modern
Harvard Press, 1993
We Have Never Been Modern
Harvard Press, 1993

Simha Arom
African Polyrhythm & Polyphony
Cambridge Press, 1991
African Polyrhythm & Polyphony
Cambridge Press, 1991
“What do African bell rhythms, spallation neutron source (SNS) accelerators in nuclear physics, Sturmian words and string theory (stringology) in computer science, Markov numbers and two-distance sequences in number theory, drawing digital straight lines in computer graphics, calculating leap years in calendar design, and an ancient algorithm (the Euclidean Algorithm in computer science) for computing the greatest common divisor of two numbers, originally described by Euclid have incommon? The short answer is: patterns distributed as evenly as possible.”
One of the oldest well known algorithms described in Euclid’s Elements (circa 300 B.C.) computes the greatest common divisor of two given integers. It is the oldest nontrivial algorithm that has survived to the present day. The idea is rather simple: repeatedly replace the larger of the two numbers by their difference until both are equal. This final number is then the greatest common divisor.
EUCLID ( m; k )
1. if k = 0
2. then return m
3. else return EUCLID ( k, m % k )
What does this have to do with music?
Mathematics and music have been formally intertwined since the day Pythagoras discovered that the pleasing experience of musical harmony is the result of ratios of small integers
2500 years ago
. However, most of this interaction has been in the domains of pitch, scales, and tuning systems. Until relatively recently rhythm’s correlation to mathematics has been mostly ignored.
Over the last few years I've spent a fair amount of time researching alternative notational systems for generative music and have found myself constantly impressed by the complexity possible within the minimal notation of ‘rhythm necklaces’ common in west African music. I read Godfried Toussaint's Geometry of Musical Rhythm and Simha Arom’s African Polyphony & Polyrhythm to help understand how these musical forms were developed. Having formally studied linear western notation I was fascinated to learn that much of the poly qualities generated in west African music came from a technique called rhythm necklaces. Underlying the technique of distributing beat emphasis in the rhythm necklace is the Euclidean algorithm.
Godfried Toussaint’s published the paper entitled Mathematical Notation, Representation, and Visualization of Musical Rhythm: A Comparative Perspective making the mathematical connections between musical rhythm and other areas of knowledge such as nuclear physics, calendar design, number theory, geometry, and computer science, as well as the work of the Greek mathematician, Euclid of Alexandria. The algorithm exposed here is a mathematical model of rhythm generation that applies to music from all over the world. Toussaint emphasizes that this is not a model of the conscious process by which musicians in any culture arrive at their preferred timelines, but rather of the inherent properties (both mathematical and musicological) of the resulting timelines obtained. I find this even more compelling because musicians’ intuition was able to lead them to a sophisticated spatio-temporal heuristic inside nature.
Benin (7,16)
F Major 7 Necklace in Four Parts
![]()
The ostinato figure pictured above is a Ghanan bell pattern visualized in Euclidean space below in the blue diagram. Each figure is identical only rotated creating the polyrhythmic necklace structure when braided together in time.
![]()
figure a.1
![]()
figure a.2
![]()
figure a.3
![]()
figure a.4
Ngbaka-Maibo (9,16)
Bb 9 Necklace in Four Parts
![]()
figure b.1
![]()
figure b.2
![]()
figure b.3
![]()
figure b.4
When the 9,16 figure is started on the penultimate onset it is the bell pattern of the Ngbaka-Maibo rhythm of the Central African Republic.
Bembé (7,12)
F Major 7 Necklace in Four Parts
![]()
figure c.1
![]()
figure c.2
![]()
figure c.3
![]()
figure c.4
![]()
A few years ago I read Bruno Latour’s
We Have Never Been Modern
and have found a striking asymmetry in his work and the cultural excavations done by Godfried Toussaint. It is astonishing that Africa's ancestors developed musical systems that were later used for many of the technical applications mentioned above. In We Have Never Been Modern I found a kinship in Latour’s ideas that discuss that there is no way of removing yourself from the experiment as an “observer.” This epistemological crisis of modernity (and thus science) formalized in Heisenberg’s uncertainty principle vindicates the pre-modern methods of Africa’s ancestors for uncovering processes latent within natural systems. The western model of linear time is derived from an ecclesiastical Christian historical account and has a distinct beginning and end. These transcendental accounts of time and history (further entrenched through Hegelian dialectics)
are fundamentally anthropogenic.
In Schelling’s words: man has history ‘not because he participates in it,
but because he produces it.’
The indigenous notion of circular time rejects anthropocentric temporality and conceives of time as unreliant upon the human or dialectical history. This desubjective model of time rests upon interdependent ecologies and doesn’t require human agency as a requisite for its existence.
Music cultivates a different set of qualities when it doesn’t follow linear dynamics. Rhythm necklaces take on a geometric recursive traits by fashioning time as a braid, fabric, or a spiral; the interlocking ostinato patterns develop trance-like characteristics when sustained. After spending extended periods internalizing the necklace techniques, the subtle iterative variances of each cycle give a strong sense of disembodiment for the listener. Being obsessed with ritual and rhythm I picked up a copy of Music & Trance: The Relations Between Music & Possession to learn about the different kinds of ritualistic uses of rhythm. Among many subjects, the book highlights the vast amount of social utility of music lost to modernity. It also emphasizes the rich practice of encoding histories and heritage
into song as an intergenerational cultural vessel. Some west Africans believe that these rhythms are transmitted from the language of the Orishas (rhythm deities) and hold magic with respect to a corresponding deity. Inside these songs ancient ancestral secrets can be unlocked by trance drumming and dance. It is remarkable that a computer scientist uncovered a Greek algorithm that uses science to denote something that has been known to non-modern tribes for millenia preceding Euclid. The permutations of repetition take listeners down tunnels of memory into focused places of trance where there are ancestral secrets encoded in rhythm.

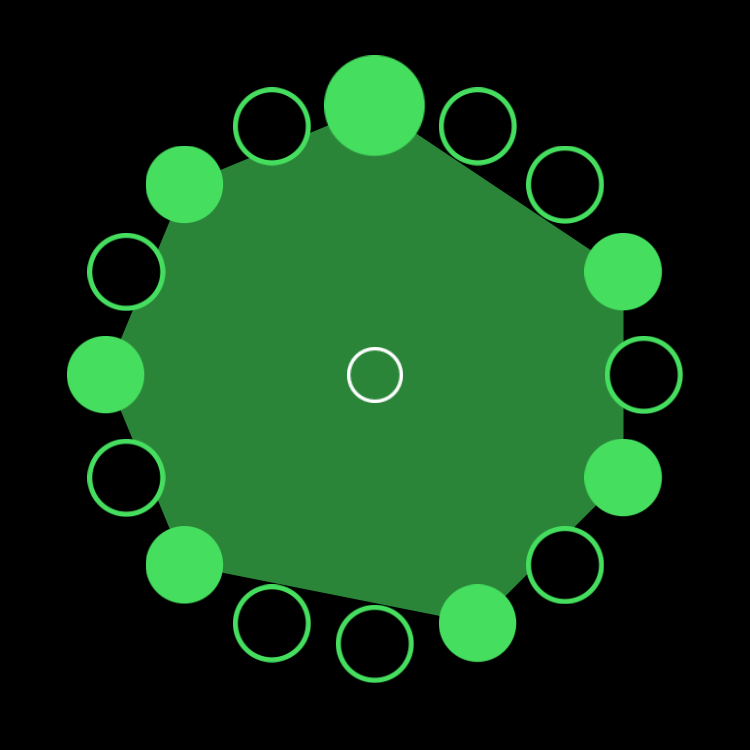
figure a.1
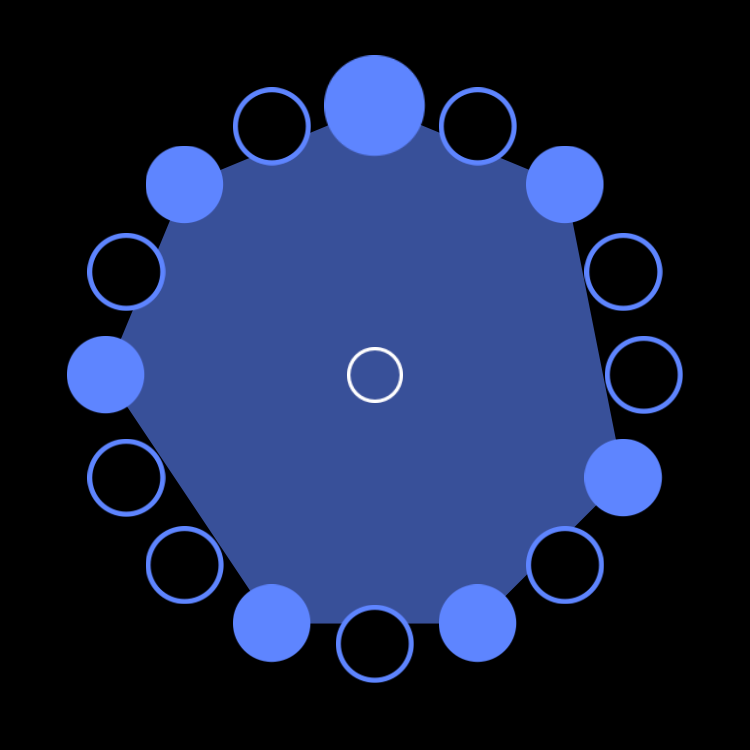
figure a.2
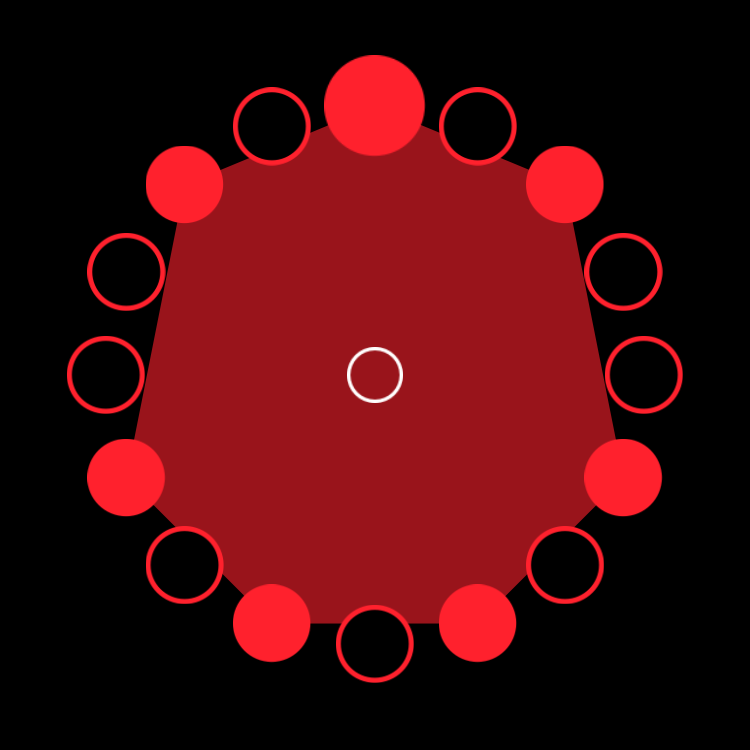
figure a.3
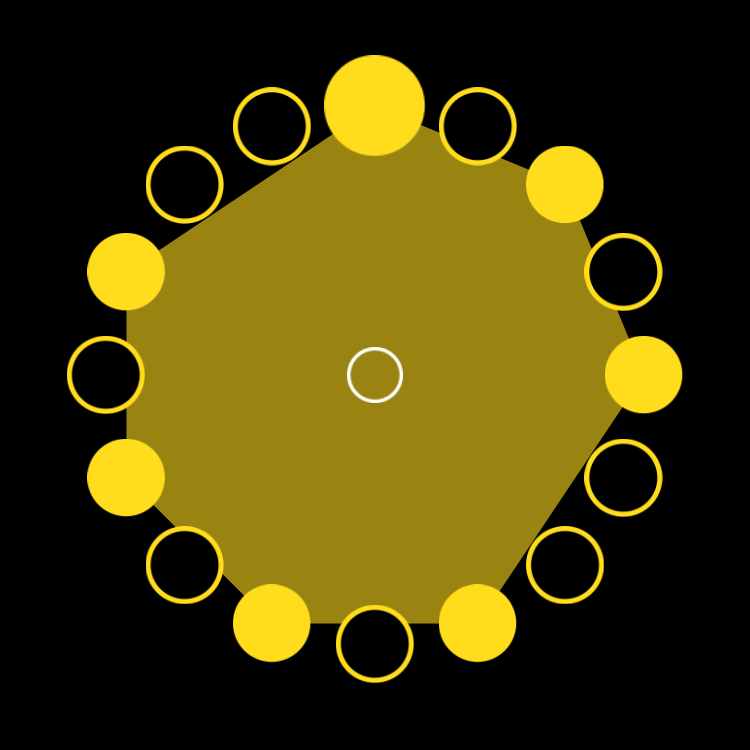
figure a.4
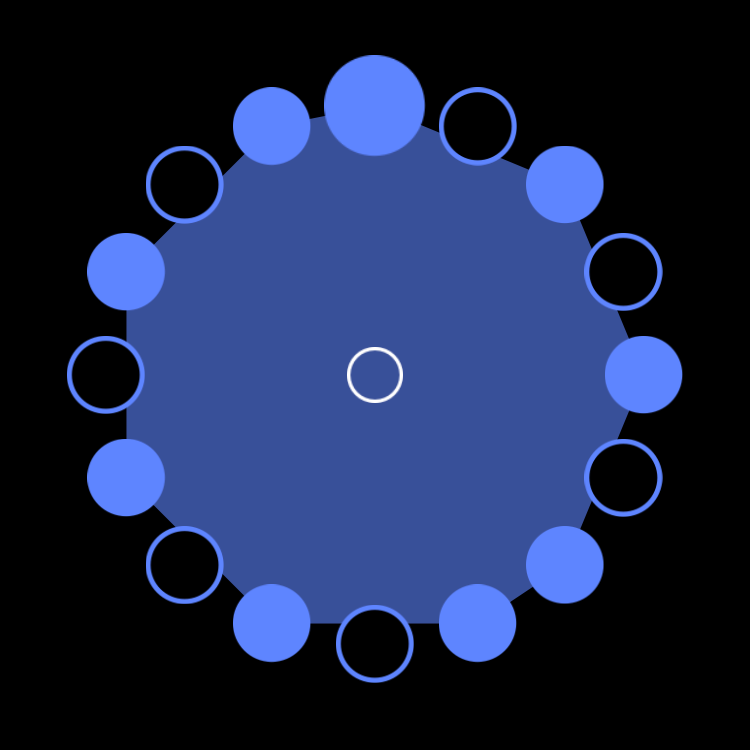
figure b.1
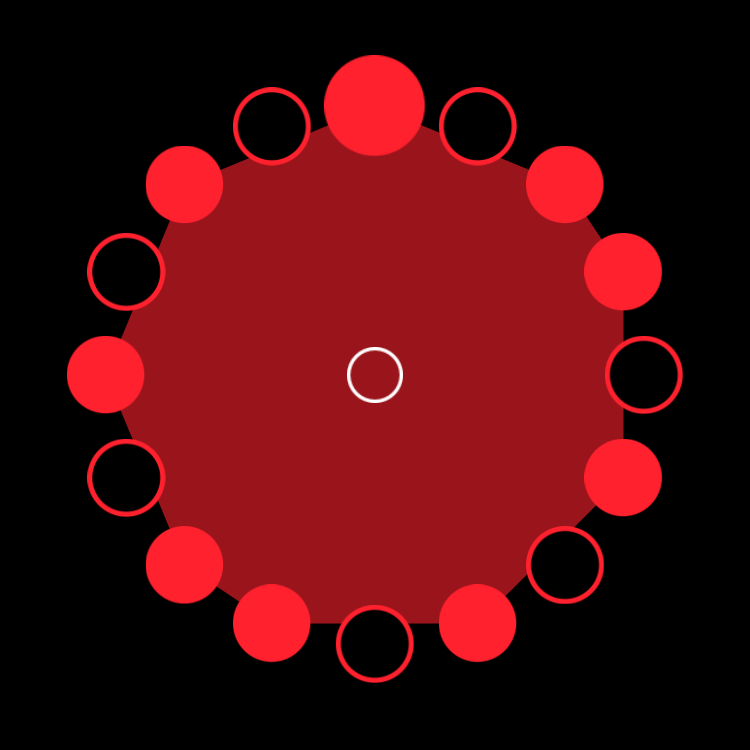
figure b.2

figure b.3
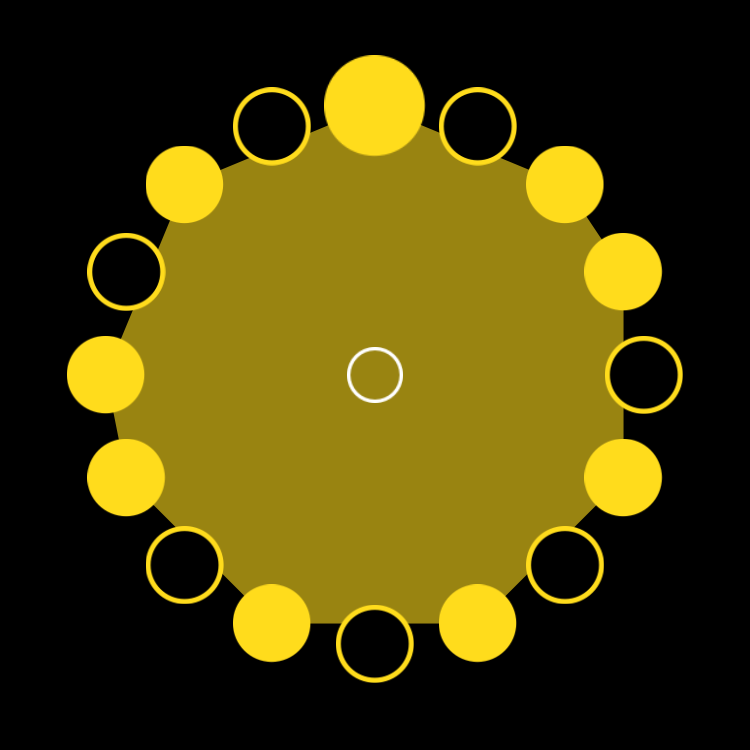
figure b.4
When the 9,16 figure is started on the penultimate onset it is the bell pattern of the Ngbaka-Maibo rhythm of the Central African Republic.
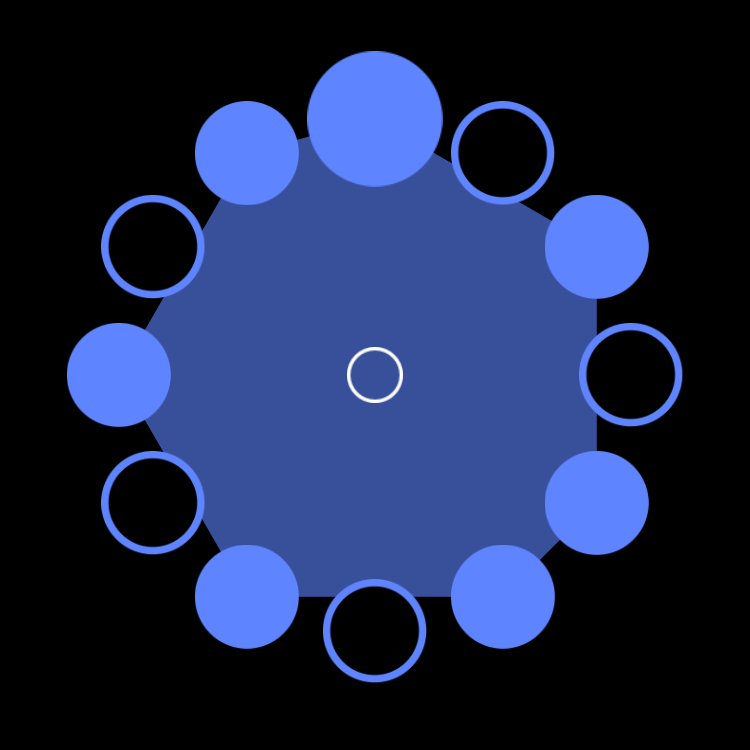
figure c.1
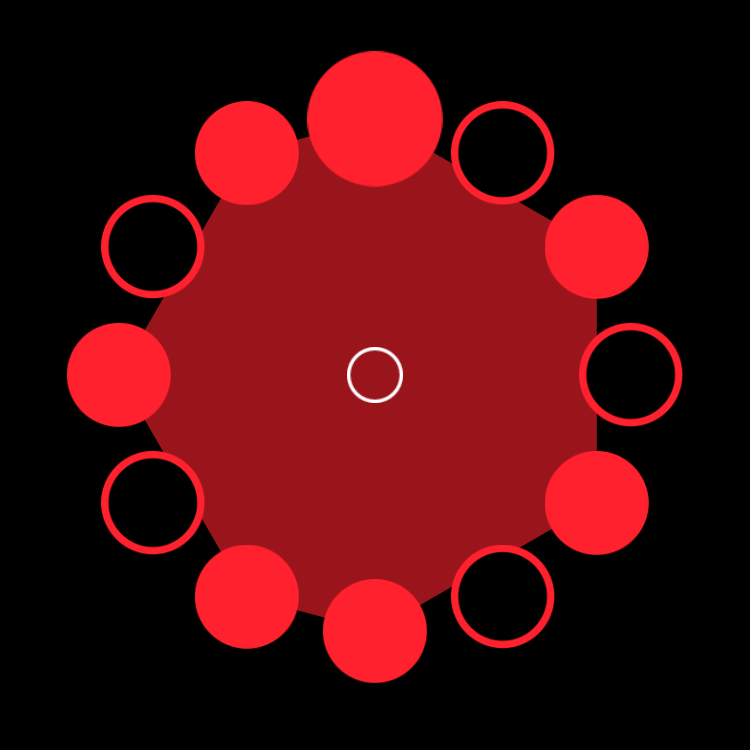
figure c.2
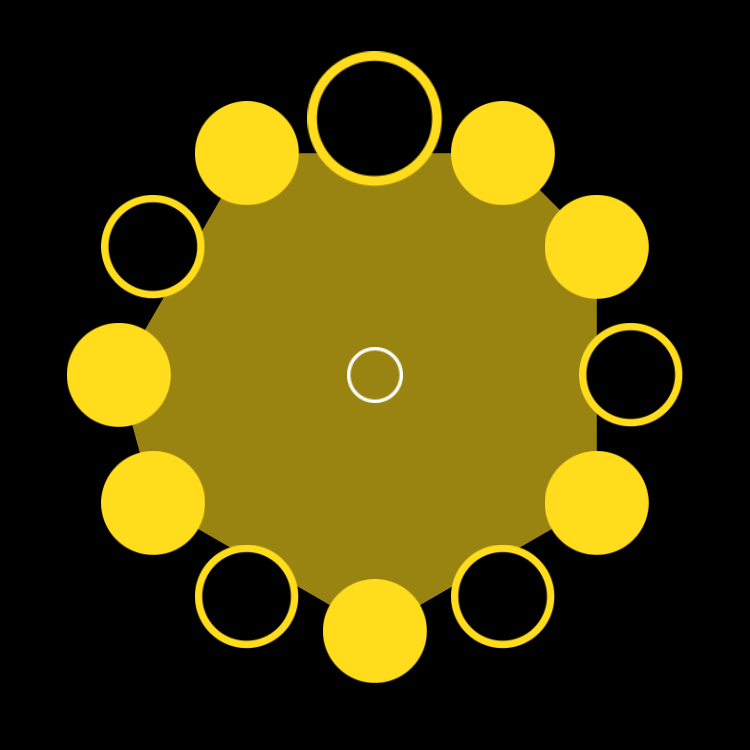
figure c.3
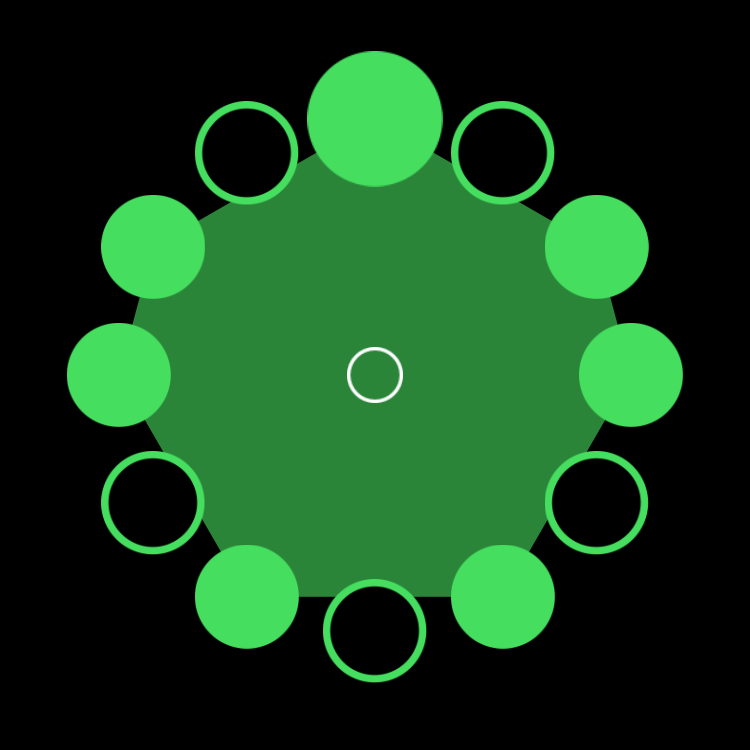
figure c.4

Resources:

Albrecht Durer
Albrecht Durer
Albrecht Durer

Godfried Toussaint’s
Geometry of Music Rhythm
CRC Press, 2013
Geometry of Music Rhythm
CRC Press, 2013